เรื่องของเรื่องคือไปดูวิดีโอของ Vertasium วิดีโอนี้ แล้วคุ้น ๆ ว่าตอนเรียนมหาวิทยาลัย ก็เคยทำอะไรแบบนี้ คือใช้ Monte Carlo ในการหาค่า Pi แต่ตอนนั้นยังไม่ค่อยเข้าใจ

เพิ่งมาเข้าใจตอนนี้

เริ่มจากลองล้างสมองก่อน ลืมไปก่อนว่าเรารู้ว่าค่า Pi เป็นเท่าไหร่ และเราต้องการหาว่าค่า Pi นั้นมันเป็นเท่าไหร่กันแน่ แบบประมาณเอาก็ได้

วิธีบ้าน ๆ แบบ Real World คือหากระดาษสี่เหลี่ยมจตุรัสมา 1 แผ่น วาดวงกลมเต็มวงลงบนกระดาษ จากนั้นเอาปากกามาสุ่มจิ้มในกระดาษ สุ่มไปเรื่อย ๆ โดยนับจำนวนจุดที่ตกลงบนวงกลม ถ้าตกบนวงกลมก็นับเก็บไว้ หลังจากสุ่มมากพอ สามารถเอาอัตราส่วนจำนวนจุดในวงกลมมาอนุมานแทนอัตราส่วนพื้นที่ของสี่เหลี่ยมกับวงกลม แล้วเอามาหาค่า Pi ได้ อันนี้วิธีแบบ Manual เลย

\[ พื้นที่สี่เหลี่ยม = พื้นที่กระดาษ (L*L)\] \[ พื้นที่สี่วงกลม = \pi*r^2 \] \[ \frac{พื้นที่วงกลม}{พื้นที่สี่เหลี่ยม} = \frac{จำนวนจุดที่ตกในวงกลม}{จำนวนจุดทั้งหมด} \] \[ \frac{\pi*r^2}{L*L} = \frac{จำนวนจุดที่ตกในวงกลม}{จำนวนจุดทั้งหมด} \] เมื่อเขียนวงกลมเต็มวงในกระดาษสี่เหลี่ยมจตุรัส จะทำให้ L=2*r \[ \frac{\pi*r^2}{(2*r)*(2*r)} = \frac{จำนวนจุดที่ตกในวงกลม}{จำนวนจุดทั้งหมด} \] \[ \frac{\pi*r^2}{4*r^2} = \frac{จำนวนจุดที่ตกในวงกลม}{จำนวนจุดทั้งหมด} \] \[ \frac{\pi}{4} = \frac{จำนวนจุดที่ตกในวงกลม}{จำนวนจุดทั้งหมด} \] หรือ \[ \pi= \frac{4*จำนวนจุดที่ตกในวงกลม}{จำนวนจุดทั้งหมด} \]

ดังนั้นเมื่อเราสุ่มจำนวนมากพอ (เอาปากกาจิ้มบนกระดาษจำนวนมากพอ) ค่า pi ที่ได้ก็จะใกล้กับความเป็นจริงมากขึ้น

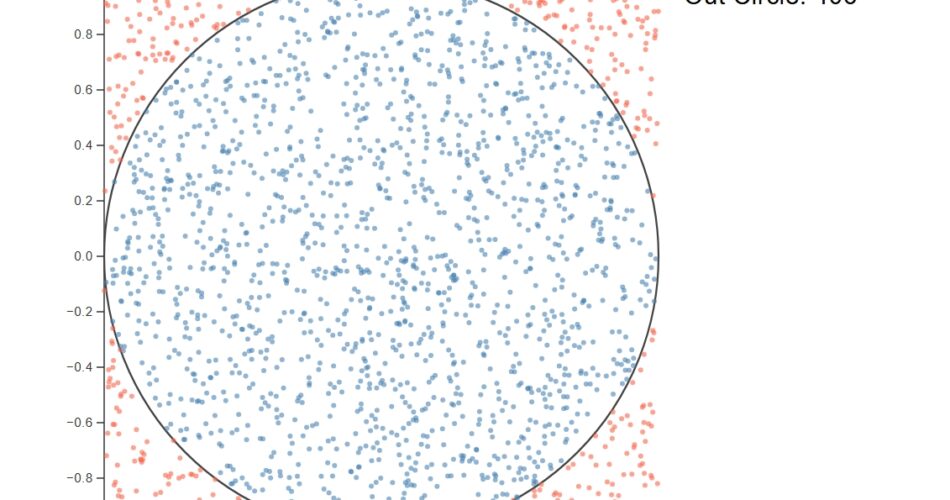
หรือถ้าขี้เกียจจิ้มเองก็ทำ Simulation ในคอมพิวเตอร์ ก็คือ สร้างสี่เหลี่ยมจตุรัสขนาด 2×2 หน่วย (ตรงกลางอยู่ที่พิกัด 0,0) จากนั้นสร้างวงกลมรัศมี 1 หน่วยไว้ตรงกลาง แล้วใช้คอมพิวเตอร์ สุ่มจุด x กับ y โดยค่าอยู่ระหว่าง -1 ถึง 1 ถ้าหาก

จากนั้นก็นำจำนวนจุดที่สุ่มนับไว้ มาหาอัตราส่วนเหมือนเดิมเลย ก็จะได้ค่า pi ที่ใกล้เคียงค่าจริง (หากมีการสุ่มมากพอ)

หรือลองเล่น Simulation ข้างล่างนี้ดูก็ได้ หวังว่าจะเข้าใจมากขึ้น (หรือเปล่านะ)

ใน Simulation จะมีการคำนวน Pi ตลอดเวลาและ plot เป็นกราฟเทียบกับจำนวนจุดที่กำลังสุ่มลงไป จะเห็นว่าเมื่อจำนวนจุดมากขึ้น ค่าที่คำนวณได้จะยิ่งใกล้ค่า pi มากยิ่งขึ้น แต่ช่วงแรก ๆ ค่าจะ Swing มาก

วิธีการนี้เรียกว่า Monte Carlo Method เมื่อสุ่มจำนวนมาก ผลลัพธ์จะลู่เข้าใกล้ค่าหนึ่ง (ซึ่งอาจเป็นค่าที่เรากำลังหาคำตอบ) ทฤษฎีวิธีการนี้พัฒนามาจาก The Rule of Large Number ซึ่งสามารถประยุกต์ใช้ในการหาคำตอบที่มีความซับซ้อนได้อีกวิธีหนึ่ง

จบ